Logic, Semantics and Verification
Logic is the study of statements of facts: how they can be combined, translated, derived and analysed. It includes what the mathematical properties of logics are, and what forms of reasoning are needed to model different kinds of systems.
Our experts study substructural and categorical logics, probabilistic systems, nominal systems and specialised systems for reasoning in particular application domains. We have particular expertise in understanding logics as mathematical structures, and in their use in verification. A key concern is logics that can be used in practice for automated reasoning, for example monadic second-order logic and logics with probability can become too complex, and one needs to identify feasible fragments.
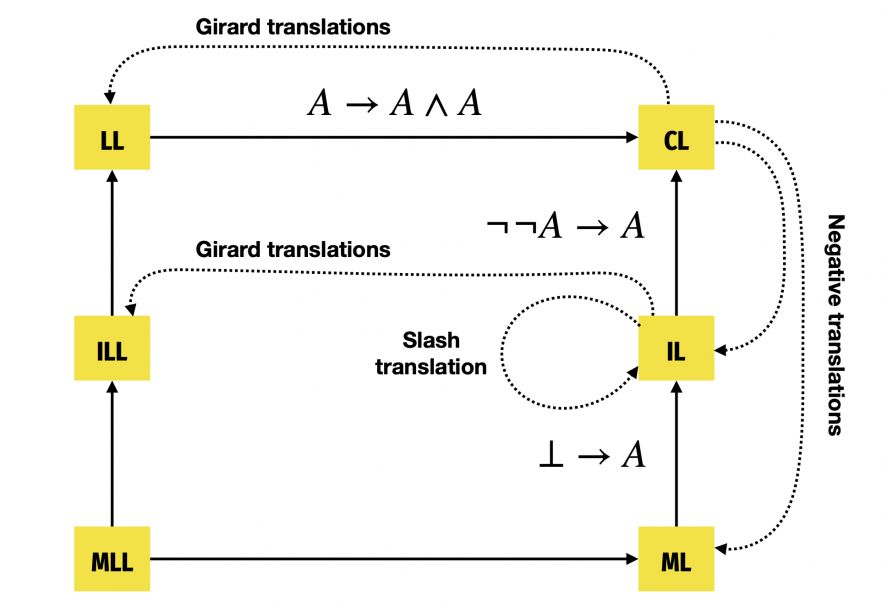
Logic-translations - author Paulo Oliva (with permission)
Probabilistic analyses are core to understanding modern systems at many levels. Useful analysis requires working computationally with classes of distributions and not simply the likelihoods of individual events. Our researchers are working on probabilistic programming languages and algorithms, using probabilistic tools to analyse the behaviour of conventional systems. We use stochastic games on graphs to model process controllers, entropy and information theory to quantify the information leakage from and hence security of programs, and innovative probabilistic AI-linked methods to generate the pseudo-random number generators used in cryptography.
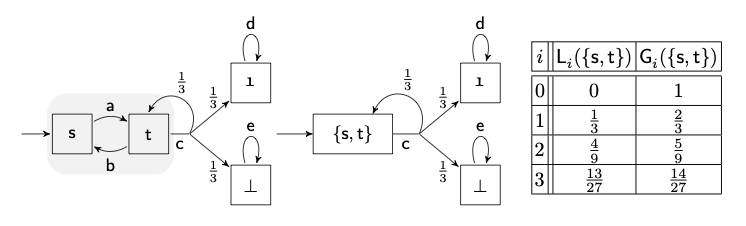
Stochastic-games - author Edon Kelmendi et al. with permission
Verification
- How can we formally describe the properties we want the system to have?
- How can we prove that our system has them?
- How can this be seamlessly integrated into the code development process?
Our researchers study a range of formal methods of software development and their application to real-world systems. These include:
- Session types: the specification and verification of communication protocols for concurrent and distributed computing based on type systems.
- Separation logic: this was the first logic to be used regularly on the entire code-bases of major companies to locate and eliminate memory violations.
- Game semantics: the use of game semantics as a verification framework for higher-order programming with effects.
Mathematical models.
Our experts study how to construct models for challenging targets such as advanced higher-order programming languages with a variety of effects or finding game and information-theoretic accounts for cybersecurity and how to characterise relations between different models of the same system.
Our researchers have been pivotal in developing such techniques as game semantics, modelling programs as a game between the code and its computational context, and have developed new forms of automata to model higher-order code, such as nominal and fresh-register automata. But they are not just concerned with building models, they also work on their validation. This approach emphasises the alignment between mathematical representations and real-world observations. Our researchers apply this rigorous approach to assess the correspondence between model assumptions and empirical data, particularly in the context of weak memory persistency models and RDMA semantics under TSO models.
By ensuring the coherence of these mathematical abstractions with practical scenarios, we strive to bolster the reliability and effectiveness of mathematical models across diverse applications.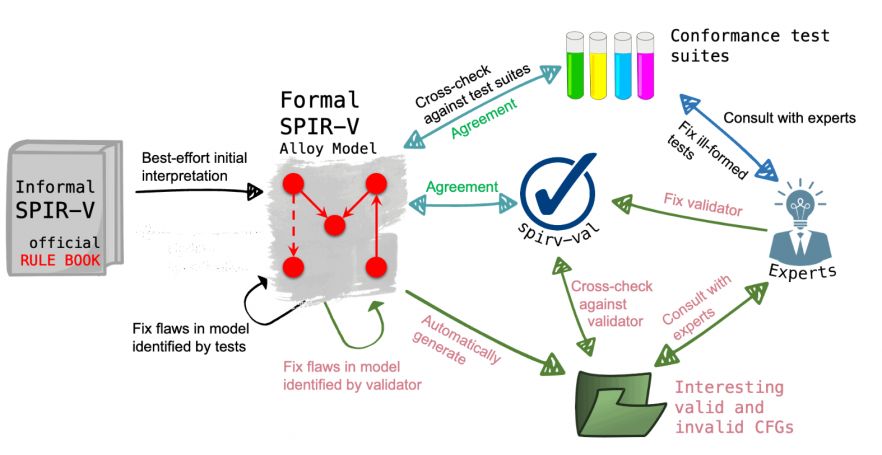
Getting a model of SPIR-V (author: Vasileios Klimis, with permission)