Modelling and Complexity

Mathematical Modelling

All formal systems are underpinned by mathematical models. Our experts study how to construct models for challenging targets such as advanced higher-order programming languages with a variety of effects or finding game and information-theoretic accounts for cybersecurity and how to characterise relations between different models of the same system.

Our researchers have been pivotal in developing such techniques as game semantics, modelling programs as a game between the code and its computational context, and have developed new forms of automata to model higher-order code, such as nominal and fresh-register automata. But they are not just concerned with building models, they also work on their validation. This approach emphasises the alignment between mathematical representations and real-world observations. Our researchers apply this rigorous approach to assess the correspondence between model assumptions and empirical data, particularly in the context of weak memory persistency models and RDMA semantics under TSO models.

By ensuring the coherence of these mathematical abstractions with practical scenarios, we strive to bolster the reliability and effectiveness of mathematical models across diverse applications.

Algorithms and Complexity

Our researchers study the inherent difficulty of computational problems on a foundational level. This entails finding links between the classification and counting of basic mathematical structures, the size of descriptions of objects and of mathematical proofs, and descriptions of algorithms and bounds for their complexity. It can involve the development of new algorithms, or rigorous mathematical proofs that certain problems cannot be solved efficiently under standard assumptions from complexity theory, such as P ≠ NP. Our researchers also specialise in modern algorithmic paradigms such as parameterised algorithms and fine-grained complexity theory.

We work closely with mathematicians in combinatorics and information theory to find and count new and complex structures and to relate them to hard instances of computational problems.

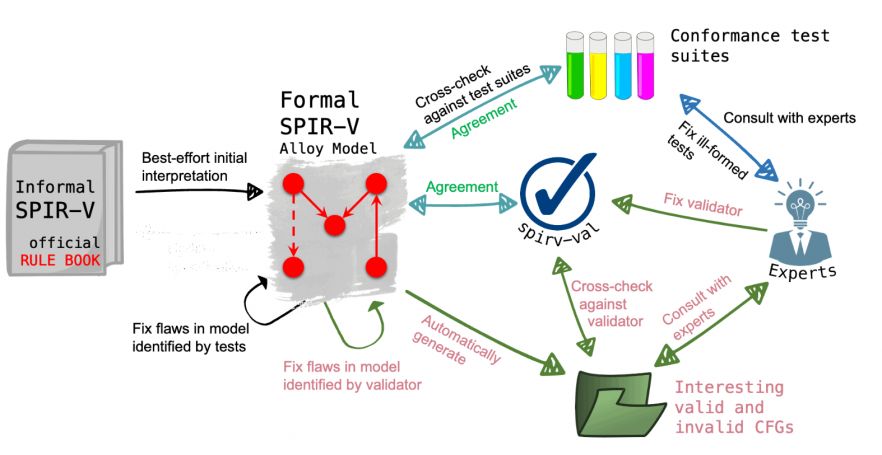
A model of SPIR-V (Klimis, with permission)

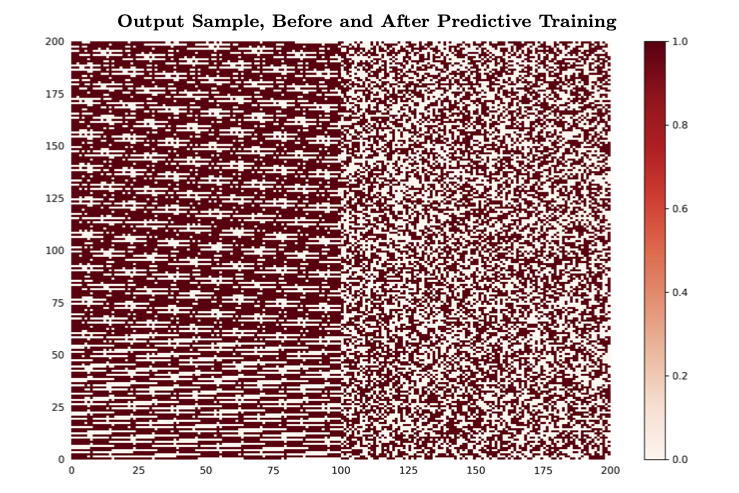
Using-adversarial-nets (Malacaria, with permission)