News

An EPSRC standard grant has been awarded to Viresh Patel (Project Lead) and Mark Jerrum (Project Co-lead) for the project "Zeros, Algorithms, and Correlation for Graph Polynomials". Read on to find out more about their plans.

This project is at the interface of theoretical computer science, mathematics and statistical physics. It aims to establish and leverage formal connections between different notions of phase transitions in these three different areas to make breakthroughs on long-standing questions. A phase transition is the phenomenon where a small change in some measure of a system (e.g. its temperature) results in a large change in its macroscopic behaviour (e.g. a material turning from a solid to a liquid). Phase transitions are currently at the forefront of study in several disciplines.

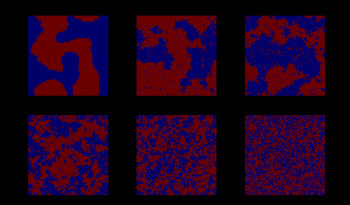
We study phase transitions in spin systems. Spin systems are networks where each node is randomly placed in one of several possible states but where the states of neighbouring nodes tend to influence each other. These spin systems exhibit remarkably rich behaviours; they originate in statistical physics, where they model gases, magnetism and other physical phenomena, but they can also help explain complex group behaviours like voting (here the vote of an individual in a social network may be correlated with the votes of their neighbours).

The partition function of a spin system is a polynomial that encodes much of the system's behaviour. A major goal in theoretical computer science and of this project is to develop fast algorithms to approximate these partition functions. The existence of such algorithms has recently been connected with the location of the zeros of partition functions, a topic of independent interest in mathematics and statistical physics since the 1950s. The project addresses several challenges here including that of understanding how strong spatial mixing for a spin system, that is the extent to which the state of a node influences the state at other distant nodes, affects the location of the zeros of its partition function.

Some of the specific highlights of the project are to attack the intensely studied problem of finding a an approximation algorithm for counting proper colourings in graphs (a.k.a configurations in the zero-temperature antiferromagnetic Potts model), to understand the algorithmic behaviour of the hardcore model when the underlying graph has some structure, to develop deterministic algorithms for approximating the Ising and monomer-dimer models, and to do all of this by understanding the zeros of the partition function in each of these cases.

We have an international project partner, Dr Guus Regts, at the University of Amsterdam, and there are several research visits planned in both directions between the groups at Queen Mary and Amsterdam, starting with PhaseCAP, a research semester programme at CWI, Amsterdam. We will also soon be advertising for a postdoc to join the project.